论文笔记--Accurate 3D Face Reconstruction with Weakly-Supervised Learning:From Single Image to Image Set
摘要
最近,基于深度学习的3D人脸重建方法在质量和效率上都显现出可喜的成果。然而,深度神经网络的训练通常需要大量的数据,而具有真实3D人脸形状标签的人脸图像却很少。该文章提出一种深度3D人脸重建方法:
利用一个稳健的混合损失函数进行弱监督学习,该函数同时考虑了 image-level 和 perception-level 的鲁棒性
( image-level损失指的是重建的人脸模型渲染得到的图片和输入图片的像素值应尽可能一致;perception-level损失指的是重建的人脸模型渲染得到的图片和输入图片的内在特征应尽可能一致 )
利用不同图像的互补信息进行形状聚合,进行多图像人脸重建。
文章提出的方法快速,准确且对遮挡和大姿态的图像具有鲁棒性。该文章在MICC Florence 和 Facewarehouse数据集上进行实验论证,同时系统地与最近几年的15种方法进行对比,实验结果证明本文提出的方法展现出了目前最先进的性能。
Code (Pytorch): https://github.com/sicxu/Deep3DFaceRecon_pytorch
介绍
从非受限场景下的2D图像中忠实地恢复人脸的3D形状是一项具有挑战性的任务,并且具有许多应用,例如人脸识别,面部媒体操控,人脸动画等。最近,人们对使用CNN来实现单个图像重建 3D 人脸的兴趣激增,以代替使用复杂且要大量优化的传统方法。由于真实的3D人脸数据稀少,以往许多方法都使用合成数据或者使用传统方法拟合的3D形状作为替代形状标签,但是这种做法会受到域差距和不准确的训练标签影响。
无监督学习的关键是一个可微的图像形成过程,它使用网络预测来渲染人脸图像,监督信号源于输入图像和渲染对应物之间的差异。该问题提出了混合级损失函数和一种新颖的基于肤色的光度误差注意策略,该方法对人脸遮挡问题有一定解决。该文章也在重点研究同一目标多图像的人脸重建问题。
该文章训练一个辅助网络。借助该网络回归得到承载身份的3D模型系数的置信度,并通过基于置信度的聚合获得最终的身份系数。它可以利用位姿差异更好地融合互补信息,学习更准确的3D形状。
该文章的主要两项贡献是:
- 提出一种基于 CNN 的单图像人脸重建方法,该方法利用混合级图像信息进行弱监督学习。改进的损失函数包括图像级损失和感知级损失。使用低维 3DMM 子空间,仍然能够胜过具有“无限制”3D 表示的现有技术。
- 提出一种用于多图像人脸重建聚合的新型形状置信度学习方法。置信预测子网也以弱监督方式进行训练,方法明显优于朴素聚合(例如形状平均)。
方法
整体架构
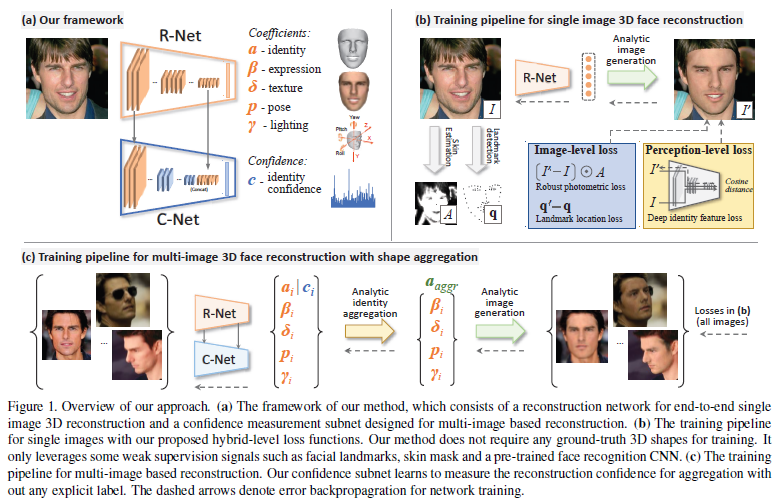
模型理念
3D face model:使用一个CNN对输入图像处理,得到\({\alpha}, {\beta}, {\delta}, {p}, {\gamma}\)等参数,\({\alpha}\in{R}^{80},{\beta}\in{R}^{64},{\delta}\in{R}^{80}\)。表达式如下所示,最终模型包括36k个顶点:
\[ S=S(\alpha,\beta)=\bar{S}+B_{id}\alpha+B_{exp}\beta\\ T=T(\delta)=\bar{T}+B_t\delta \]
\({S}, {T}\)分别表示平均脸的形状和纹理参数,\(B_{id}, {B_{exp}}, {B_t}\)分别是身份,表情和纹理的PCA基(都经过标准偏差归一化处理);使用BFM预测\(\bar{S},B_{id},\bar{T},B_t\),使用FaceWarehouse预测\(B{exp}\)。
Illumination Model:假设人脸是Lambertian平面,使用球谐函数SH估计场景光照。法向是\(n_i\),皮肤纹理是\(t_i\)的顶点\(s_i\)辐射度为下式,其中\({\phi_b}:R^3\rightarrow{R}\)是SH基函数,\(\gamma_b\)是对应的SH系数,\(\gamma\in{R}^9\),\(B=3\) \[ C(n_i,t_i|\gamma)=t_i·{\sum}_{b=1}^{B^2}{\gamma_b}{\phi_b}(n_i) \] Camera Model:透视投影,3D人脸姿态\(p\)由旋转\(R\in{SO(3)}\)和平移\(t\in{R^3}\)表示。
Summary:最终预测的向量结果\(x=(\alpha,\beta,\delta,\gamma,{p})\in{R^{239}}\),(备注:80+64+80+9+6=239)利用ResNet50来回归预测这239个参数,将ResNet50的最后一层全连接输出改为239,该网络称为R-Net。
单张图片人脸重建
给定一张RGB图片\(I\),作者使用R-Net回归参数向量\(x\),根据得到的人脸模型可以渲染得到新的图片\(I'\),训练时不需要任何真实标签,而是根据\(I'\)来计算损失。
Image-Level Loss
Robust Photometric Loss
原始图片和重建图片之间的像素差异作为损失是直观的方法,本文基于此提出了一种鲁棒的、皮肤感知的图像损失:式子定义如下:
\[ L_{photo}(x)=\frac{\sum_{i\in{M} }A_i·||I_i-I'_i(x)||_2}{\sum_{i\in{M} }A_i}\\ \]\[ A_i=\begin{cases} 1 & P_i>0.5\\ P_i & otherwise \end{cases} \] 其中\(i\)表示像素索引;\(M\)表示投影的人脸区域;\(||·||\)表示\(l_2\)距离;\(A\)是一个基于皮肤颜色的attention mask,借助在一个皮肤数据集训练好的贝叶斯分类器来预测每个像素\(i\)上的皮肤颜色概率\(P_i\) 。
Lamdmark Loss
在训练中使用2D图片上的人脸关键点作为弱监督信息,利用sota的3D人脸对齐方法来检测训练图片的68个人脸坐标\(q_n\),将重建人脸的3D关键点投影到图像空间得到\(q'_n\),计算两者的距离作为损失。\(w_n\)是坐标点权重,经过实验发现在嘴巴内部和鼻子处的权重设为20,其他地方的权重设为1最合适,式子如下。
\[ L_{lan}(x)=\frac{1}{N}{\sum}_{n=1}^{N}w_n||q_n-q'_n(x)||^2 \]
Perception-Level Loss
\[ L_{per}(x)=1-\frac{\left<f(I),f(I'(x))\right>}{||f(I)||·||f(I'(x))||} \]
正则化
为防止人脸形状和纹理退化,使用3DMM系数的正则项:
\[ L_{coef}(x)=w_{\alpha}||\alpha||^2+w_{\beta}||\beta||^2+w_{\gamma}||\gamma||^2 \\ w_\alpha=1.0 \quad w_\beta=0.8 \quad w_\gamma=1.7e-3 \]
尽管BFM模型的面部纹理是使用特殊设备获得的,但仍有一些阴影(如环境光遮蔽),为此再添入一个正则项:
\[ L_{tex}(x)=\sum_{c\in{r,g,b}}var(T_{c,R}(x)) \]
损失函数总结
损失函数的总式子如下,其中\(w_{photo}=1.9 \quad w_{lan}=1.6e-3 \quad w_{per}=0.2 \quad w_{coef}=3e-4 \quad w_{tex}=5\) \[ L(x)=w_{photo}L_{photo}(x)+w_{lan}L_{lan}(x)+w_{per}L_{per}(x)+w_{coef}L_{coef}(x)+w_{tex}L_{tex}(x) \]
多张图片人脸重建
除了从单张人脸图片重建人脸,如何从一个人的多张脸部图片,去重建一个更加精确的人脸模型也是一个很有意义的问题。不同的图片可能采集自不同的姿态、光照等,能够互相提供补充信息,这样重建出来的人脸对于遮挡、不佳的光照等情况更加鲁棒。

作者从单张图片人脸重建的结果学习一个置信度(反映重建质量),作者针对人脸形状参数\(\alpha\in{R^{80}}\)生成一个反映置信度的向量\(c\in{R^{80}}\),图片集为\(I:=\{I^j|=j=1,...M\}\),最终的人脸形状参数为:
\[ a_{aggr}=(\sum_{j}c^j\odot\alpha^j)\oslash(\sum_jc^j) \]\[\odot和\oslash分别表示哈达玛积和商 \]
作者提出C-Net来预测置信度\(c\),由于R-Net能够预测诸如人脸姿态、光照等高阶信息,很自然地想到将其特征图运用到C-Net中来,作者同时使用了R-Net的浅层和深层特征,如前图所示。为了训练C-Net,首先从一张图片\(I^j\)得到人脸系数\(\hat{x}^j\),\(\hat{x}^j=(\alpha_{aggr},\beta^j,\delta^j,\gamma^j,p^j)\),然后生成重建图片\(I^{j'}\),C-Net的损失函数如下所示,\(L(·)\)是前面单张人脸图片重建的损失函数
\[ \mathcal{L}(\{\hat{x}^j\}) = \frac{1}{M}\sum_{j=1}^{M}L(\hat{x}^j) \]